СОВЕТ 3. Принцип отсечения ложных гипотез*, или «Не вырой себе яму!»

Решая задачи, делаешь различного рода предположения (гипотезы). Главное, чего здесь следует опасаться, — это пойти на поводу у ложной гипотезы. Есть риск потратить много усилий, добиваясь успеха в заведомо безнадежном деле.

Пример 9

Основанием пирамиды является трапеция с основаниями a и b (a >b) и высотой h. Грань пирамиды, проходящая через меньшее основание трапеции, перпендикулярна плоскости основания. Противолежащая грань является равнобедренным треугольником с углом a при вершине пирамиды.

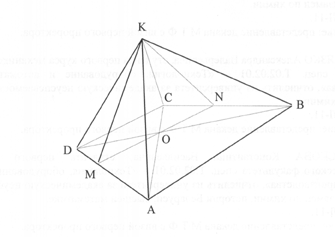
Рис.2

Через точку пересечения диагоналей основания и вершину пирамиды проведена плоскость, параллельная основаниям. Найти площадь треугольника, получившегося в сечении.
Многие абитуриенты ошибочно считали, что прямая, по которой плоскость пересекает основание пирамиды, является средней линией трапеции. После этого предположения дальше можно было уже не суетиться. (Проверь свои силы, решив эту задачу самостоятельно!)
Отсечение ложных гипотез можно осуществлять, пользуясь «методом вариации параметров». Так, если в нашей задаче изменить длины боковых сторон и оснований трапеции (сделав для наглядности несколько чертежей на черновике), то станет совершенно очевидным, что отрезок, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, вовсе не должен быть средней линией.
Для отсечения ложных гипотез может пригодиться и «метод от противного». Надо допустить, что рассматриваемое утверждение верно, и посмотреть, к каким последствиям это приведет. (В нашей задаче трапеция превратится в параллелограмм.)
Если же ты сомневаешься в истинности некоторой формулы, то проверь ее на числовых примерах. (Поставь маленький эксперимент и попытайся найти «щель» — контрпример.) Помни, что если формула неверна хотя бы в одном случае, то она неверна вообще!!!

А теперь — поучительная таблица (надеюсь, что она тебе пригодится) для упражнений такого сорта.

Формулы этой таблицы являются источниками многих ложных гипотез. Например, при виде уравнения 4^x + 6^x = 2 * 9^x некоторые храбрецы смело заявляют: «А я сейчас как возьму логарифм от обеих частей, так сразу все и прояснится!» Ясно, что эта надежда основана на шестой формуле таблицы. (В действительности, для решения этого уравнения надо разделить обе части на любую из входящих в него степеней.)
Скажем здесь же о феномене, который я называю «ложные» обозначения. Достаточно в задаче, особенно геометрической, ввести неудачные (иногда это избыточные) обозначения, и быстро идешь в тупик. А единственный выход из тупика — вернуться назад, что приводит к ненужным затратам времени.
Ложные гипотезы создает иногда сама наша рука, порой рисуя вместо произвольного треугольника равнобедренный или даже равносторонний, а в прямоугольном треугольнике гипотенузу равной катету. Такой чертеж создает непреодолимые трудности, направляя нас по вектору психологической инерции в другую сторону.
С задачей надо обращаться нежно, не навязывая ей своей воли. При этом может оказаться полезным «принцип наибольшей общности или наихудшего случая», название которого говорит само за себя. Так, если в задаче речь идет о пирамиде, то вовсе не обязательно, чтобы она была правильной; центр вписанного в пирамиду шара вовсе не обязан лежать на высоте пирамиды. Если же пирамида правильная, то центр вписанного в нее шара действительно лежит на ее высоте, но не совпадает с серединой высоты и т. д.
Принцип отсечения ложных гипотез тесно связан с более общим принципом, изложенным в следующем пункте.

* Гипотеза — происходит от греческого слова «предположение». Гипотезой обычно называют предположение о связи, или причинах, или зависимостях между наблюдаемыми явлениями. С помощью гипотез часто пытаются раскрыть внутренний механизм таких явлений. Так же как и принцип, гипотеза играет чрезвычайно важную роль в построении теории. (Томилин А. Н. В поисках первоначального. — Ленинград: Детская литература, 1978. — С. 146.)

СОВЕТ 2. Принцип правильности решения, или «Чувство опасности»