СОВЕТ 2. Принцип правильности решения, или «Чувство опасности»

Математика — это игра по правилам, в соответствии с которыми строятся необходимые логические цепочки. Каждое нарушение любого из правил — ошибка, которая обычно приводит к пагубным последствиям. (Именно это имел в виду один древний философ, утверждая, что математика — наука свирепая?) Так, если в диктанте по русскому языку, сделав две орфографические и две синтаксические ошибки, ты можешь получить оценку четыре, то в контрольной работе по математике, состоящей из пяти задач, наличие по одной ошибке в каждой из них, приведет, очевидно, к оценке два. Особый бич абитуриентов — ошибки типа описки. Ты и сам прекрасно знаешь, что достаточно один раз ошибочно заменить знак «плюс» на знак «минус» — и дальше можно уже никуда не спешить, ибо все последующие правильные действия приведут скорее всего к неверному результату. Недаром математики уважают афоризм: «Хочешь делать быстро — делай правильно!»
Согласно З. Фрейду, некоторые описки и ошибки совершаются человеком на подсознательном уровне, и поэтому обнаружить их самому часто очень трудно. Отсюда вытекает необходимость как локального контроля (каждый шаг в решении проверяй дважды), так и глобального (проверка результата решения, хотя бы частичная, на правильность и реальность).

Пример 6

Решить уравнение: cos x + sin x = 1.

Решение

Приведем четыре способа.

Первый способ (часто встречающийся в абитуриентской практике). Возведем обе части уравнения в квадрат. Имеем:

cos²x + sin²x + 2cosx sinx = 1 > 1 + sin2x = 1 > sin2x = 0 >
Но решение, увы, не окончено, ведь было использовано возведение в квадрат, которое может привести к посторонним корням. Поэтому проверка — обязательный этап решения. Нетрудно понять, что проверке подлежат числа из множества
Подставляя их в исходное уравнение, убедимся, что только 0 и является решениями. Значит, ответ записывается так:

Второй способ основан на формуле
(это одна из двух часто применяемых формул «понижения степени». А вот и вторая:
Имеем:

В этом месте абитуриент с радостью сокращает обе части уравнения на теряя при этом группу решений
Это грубая ошибка! Берегись ее!
Надо действовать так. Сократив обе части уравнения на 2, перенесем все в левую часть и разложим на множители:

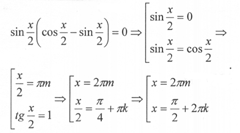
Решая уравнение мы делим обе его части на
Это корректный шаг, ибо предложение влечет за собой Откуда следует, что что противоречит основному тригонометрическому тождеству
Кстати, решив уравнение двумя разными способами, мы тем самым осуществили глобальный контроль результата. А это уже некоторая гарантия его правильности.

Третий способ. Преобразуем левую часть уравнения:

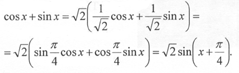
Теперь имеем:

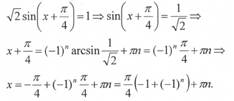
Если n = 2k, то
Если же n=2k + 1, то

Четвертый способ. Воспользуемся универсальной подстановкой

Далее имеем:

где

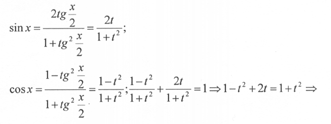
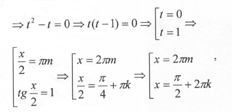
Примечание: «Метод рационализации».

Использованный в четвертом способе подход применяется для преобразования тригонометрических выражений, содержащих синусы и косинусы одного аргумента (в частности, при интегрировании).

Соответствующие формулы легче вывести, чем запомнить.
Действительно,

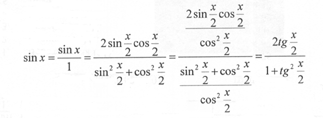
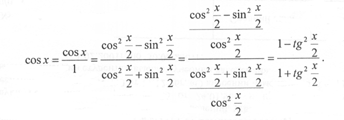
К сожалению, метод рационализации содержит один подводный камень. А именно: функции cos x и sin x определены для всех действительных значений x, а функция определена при условии
Это может привести к потере решений. Например, в уравнении
sin x — cos x значения являются решениями, которые мы потеряем, используя универсальную подстановку. К счастью, в примере 6 этого не происходит.

Пример 7

Решить уравнение:

|x — 1| + |x + 1| = 2.

Решение

«Метод интервалов».

Шаг 1. Найдем корни подмодульных выражений.
x — 1 = 0 > x = 1; x + 1 = 0 > x = — 1.

Шаг 2. Отметим их на координатной прямой. Координатная прямая разбилась при этом на три части «интервала». Корни исходного уравнения, будучи действительными числами, либо попадают в один из полученных интервалов, либо совпадают с их концами.

Шаг 3. Рассматриваем уравнение на интервалах.

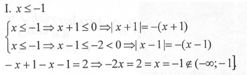
Значит, x = — 1 есть корень исходного уравнения. (Проверь подстановкой!)

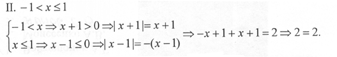
Значит, каждое число из интервала ( —1;1] является решением.

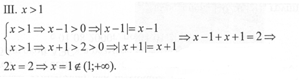
Значит, на данном интервале решений нет.

Шаг 4. Остается «собрать урожай», объединив решения из интервалов:

Примечание
1. Первый вопрос, который задают учащиеся: «Почему необходимо рассматривать именно корни подмодульных выражений?» Ответ прост. Функции у = х — 1; у = х + 1, стоящие под модулями, — линейные и нуль каждой из них разделяет область значений функции на интервалы знакопостоянства. (Докажи это самостоятельно!) Кстати, этим фактом объясняется «скоростной» вариант метода интервалов, при котором доказательство подменяется проверкой знака подмодульного выражения в одной точке из рассматриваемого в данный момент промежутка. Без соответствующего обоснования такая процедура не носит доказательной силы. В более сложных ситуациях это может оказаться небезопасным.
2. Что касается концов интервалов, то их можно, конечно, включать в интервалы по-разному. Но я делаю так: левый конец исключаю, правый — включаю, чтобы избежать дублирования. Между прочим, при построении графиков методом интервалов дублирование концов полезно.
3. В рассмотренном примере полная проверка результата решения, понятно, невозможна (нельзя подставить все числа отрезка [— 1; 1] в исходное уравнение). Поэтому на черновике желательно выполнить частичную проверку, взяв хотя бы по одному представителю для каждого из трех интервалов, участвующих в решении.
4. Решение примера можно несколько упростить, если заметить, что функция |x — 1| + |x + 1| четная и, значит, считая x > 0, вместо трех интервалов получим два:

Пример 8

Упростить выражение:

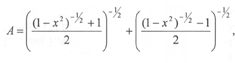
если причем n > 1.

Решение

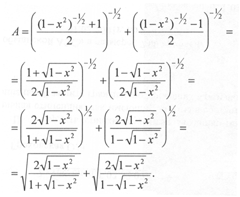
Определим значение 1 — x² при заданном значении x:

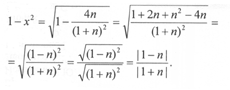
Здесь самое время поставить табличку «СТОП!». Последний переход в решении основан на формуле Эта формула — «проклятие абитуриентского рода». Если подсчитать, скольким людям она «подставила ножку», то получится «сумасшедшее число». ПОМНИ ЭТО!

Преодолев данное скользкое место, легко завершаем решение. Так как n > 1, то
Но из n > 1 следует, что — n < —1 и 1 — n < 0, значит,
|1 — n| = — (1 — n) = n — 1. Поэтому

Окончательно имеем:

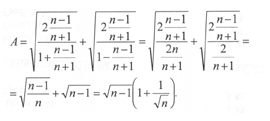
При решении примеров на упрощение выражений не следует забывать об области определения. В рассмотренном примере она задается условиями:
Легко доказать, что при х = требуемые неравенства действительно имеют место, если n > 1.

Безусловно, принцип правильности решения — это основное требование, предъявляемое к решению. Поэтому еще раз хочу предостеречь тебя от ошибок-описок, которые подстерегают буквально на каждом шагу. Например, достаточно в условии задачи случайно изменить один из параметров и, как правило, ты вместо «ручной» задачи, допускающей красивое решение, получаешь «дикую», которая вообще не решается элементарными методами. Это как поэзия и проза: если заменить одно слово в четверостишии, то исчезает гармония.
Наряду с ошибками-описками, бывают «зверьки» и пострашнее. При их отлове понадобятся хорошие «капканы» (см. советы 3, 4, 5).

ЧАСТЬ 1

СОВЕТ 3. Принцип отсечения ложных гипотез*, или «Не вырой себе яму!»