ЧАСТЬ 1

«Хороший совет не имеет цены».

Пословица

СОВЕТ 1. Принцип* отсроченного действия, или «Спешите медленно!»

Представь себе, что под грудой камней спряталась мышь, которую необходимо поймать. Конечно, можно начать камень за камнем разбирать мышиное укрытие. Правда при этом мышка может из него убежать. Гораздо лучше обойти груду и внимательно посмотреть: не покажется ли где-нибудь хвостик мышки. Тогда до поимки ее останется самая малость.
После прочтения условия задачи первое желание, которое часто возникает — это не решать ее. Пойди на поводу у этого желания. Повремени с преобразованиями и другими действиями. Возможно, именно в этот момент «живого созерцания», ты подметишь полезную закономерность, которая в дальнейшем существенно повлияет на решение. Если данный этап, увы, не принес плодов, то не огорчайся, а попытайся найти область определения, или хотя бы некоторое множество, ее содержащее. Полученная информация может значительно уменьшить неопределенность задачи и привести к быстрому решению. Кроме того, при отыскании области определения глубже проникаешь в структуру задачи, что иногда помогает установить неожиданные связи.
(Напомним, что квадратные скобки [ ] используют, когда отыскивают объединение множеств решений, а фигурные { } — пересечение.)

Пример 1

Решить уравнение:

Решение

Не будем спешить возводить обе части уравнения в квадрат, а найдем область определения:

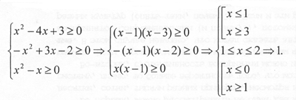
Подставляя x = 1 в исходное уравнение, убеждаемся, что это и есть единственный корень.

Пример 2

Решить уравнение:

Решение

Опять воздержимся от возведения в квадрат обеих частей уравнения. Немного поразмыслив, получим:

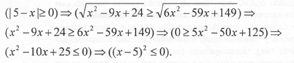
Но, с другой стороны, (х — 5)² > 0, ибо квадрат любого числа неотрицателен. Теперь из системы следует, что x = 5.
Легко убеждаемся, что это и есть единственный корень исходного уравнения.

Замечание: «Эффект Змея Горыныча».

Попробуем решать исходное иррациональное уравнение стандартным методом. Для этого возведем обе части уравнения в квадрат в надежде, что в конце решения нам удастся выявить посторонние корни с помощью проверки. Имеем:

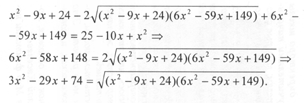
Далее необходимо обе части полученного уравнения опять возвести в квадрат, что, очевидно, приведет к еще большему «разбуханию» выкладок. Это явление я называю «Эффектом Змея Горыныча» (надеюсь, что ты помнишь сказку о коварном Змее, у которого вместо срубленной головы тотчас вырастали две или три новые). Как правило, наличие «Эффекта Змея Горыныча» связано с тем, что ты идешь по той ветви «веера возможностей», которая ведет в тупик. Поэтому необходимо вернуться к условию задачи и искать другое решение.

В процессе решения почаще задавай себе вопрос: «А нельзя ли здесь сделать по-другому?» Может оказаться, что это другое проще!

Пример 3

Решить неравенство:.

Решение

Начнем с области определения

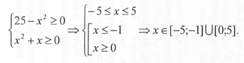
Далее возведем обе части неравенства в квадрат. (Это возможно ввиду их неотрицательности.)

Типичная ошибка, которая здесь обычно совершается, состоит в возведении обеих частей полученного неравенства в квадрат без предварительной проверки их на неотрицательность (смотри: 2 > — 3, но 2² = 4 < 9 = (— 3)²).

Вернемся к области определения. Имеем:

Но
Значит, неравенство выполняется сразу для всех x из области определения. Поэтому множество исходного неравенства есть [— 5; — 1] U [0; 5].

Замечание

ПМЛИ. Как справедливо утверждает Роберт Уилсон: «Мудрым будь — обобщить не забудь!». Так вот, в решении примеров 1, 2, 3 присутствует некоторая общая идея, которую я называю Принципом Максимума Локальной Информации (ПМЛИ): на каждом шагу процесса поиска решения необходимо стремиться к получению максимальной информации из структуры полученной ситуации («выжимай» максимум информации из полученной ситуации).

Как видно из решений примеров, ПМЛИ иногда способствует отсечению ненужных ветвей «веера возможностей» (точнее, веера возможных дальнейших шагов), который, как правило, необходимо строить после каждого шага в процессе поиска решения. Схематически веер возможностей можно изобразить так:

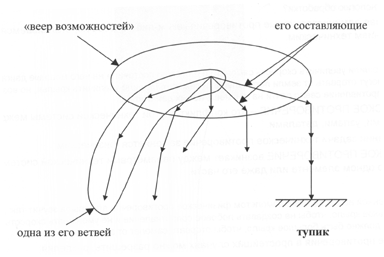
Рис. 1

А для острастки нет ничего лучше сказки. Ехал однажды вечером богатырь Илья Муромец дремучим лесом по длинной-длинной дороге. Ехал он, ехал и, наконец, приехал к развилке, из которой выходили три дороги. На большом придорожном камне было нацарапано следующее: «Налево пойдешь — могилу найдешь; направо пойдешь — к Яге попадешь, а прямо пойдешь — никуда не придешь!» «Какая ни Яга, а все-таки Баба», подумал Илья Муромец и повернул коня направо.

Внимание — задание

Установить, кто сделал надпись на камне.
Достроить «веер возможностей» Ильи Муромца так, чтобы он имел не менее 5 составляющих.

Пример 4

Решить систему неравенств:
.

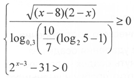Решение

Несмотря на очевидную простоту второго неравенства системы, не будем пока его трогать, а займемся первым.

Шаг 1. «Экспериментальная стадия»
Начнем с числителя. Нетрудно заметить, что числа 2 и 8 являются решениями первого неравенства.

Шаг 2. Оценим число стоящее в знаменателе. Имеем:

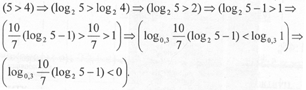
Шаг 3. Итак, в знаменателе первого неравенства системы отрицательное число. Значит, и числитель (ввиду неотрицательности дроби) должен быть числом неположительным, т. е. Но с другой стороны, квадратный корень неотрицателен по определению, т. е.
Сравнивая последние неравенства, получаем, что

и других решений первое неравенство не имеет.

Шаг 4. Непосредственной подстановкой чисел 2; 8 в неравенство:
2^х—3 — 31 > 0, убеждаемся, что только число 8 удовлетворяет обоим уравнениям системы.

Примечание: «Эффект границы».

Найдем область определения системы. Очевидно, она совпадает со множеством решений квадратного неравенства: (х — 8)(2— х) > 0. Откуда следует, что .
А как мы только что установили, х = 8 и является решением нашей задачи, т. е. решение совпадает с одним из концов области, которой оно принадлежит. Такая ситуация встречается в математике достаточно часто (например, при исследовании функции f(x), непрерывной на отрезке [a, b], на наибольшие и наименьшие значения). Поэтому, естественно ее как-то назвать. Подходящий термин, по-видимому, и есть «эффект границы». А теперь — рецепт на будущее: в соответствии с «эффектом границы» рекомендуется изучить поведение исследуемого объекта на границе «вследствие того упрямого факта, что весьма часто решение является граничной точкой области изменения переменных». (Беллман Р. Динамическое программирование. — М.: Изд. иностранной литературы, 1960. — 400 с. — С. 9.)

Пример 5

Найти все значения параметра , при которых система имеет одно решение.

Решение

Обратив внимание на то, что в каждое из уравнений системы x входит четным образом (другими словами, каждая из функций
2^|х| + |x| — y — x² — a и (x² + y² — 1) является четной относительно переменной x), приходим к выводу, что если пара (x, y) является решением системы, то и пара (— x, y) также является решением. Ввиду требования единственности решения, эти пары должны совпадать:
(x, y) = (—x, y) > x = —x > 2x = 0 > x = 0.

Подставляя это значение x в систему, получим

Докажем, что при a = 0 система действительно имеет единственное решение.

Второе уравнение системы задает окружность с центром в начале координат радиуса 1. Поэтому геометрически видно, что
|x| < 1, |y| < 1. Покажем это аналитически. Имеем: y² = 1 — x²; далее
x² > 0 > — x² < 0 > 1— x² < 1. Следовательно, у² < 1. Отсюда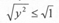
и |y| < 1. В уравнение x² + y² = 1 переменные x, y входят симметрично. Значит, аналогичное утверждение справедливо и для x.
Пусть a = 0. Тогда первое уравнение системы принимает вид:
2^|x|+ |x| = y + x². Откуда 2^|x| = x² — |x| + y < x² — |x| + 1, ибо
y < |y| < 1 (см. п. 1).
Покажем, что |x| < 1, отсюда следует x² — |x| + 1 < 1. В самом деле, x² — |x| + 1 < 1, отсюда x² — |x| < 0 и далее
- |x|(|x| — 1) < 0. Но |x| > 0, а |x| — 1 < 0 и требуемое утверждение доказано.
Из п.п. 2-3 получаем
2^|x| = x² — |x| + y < x2 — |x| + 1, отсюда получаем 2^|x| < 2⁰, отсюда |x| < 0, ибо при основании большем 1 показательная функция монотонно возрастает. Но |x| > 0. Следовательно, x = 0 и, значит, равенство 2^|x| = x² — |x| + y возможно только при одном значении x. Подставляя x = 0 в уравнение 2^|x| = x² — |x| + y, получим y = 1. Итак, данное уравнение имеет единственное решение (0; 1) при условии, что x² + y² = 1. (Очевидно пара (0; 1) является решением и уравнения x² + y² = 1.)
При a = 2 пары (1; 0), (— 1; 0) и (0; — 1) являются решениями исходной системы, в чем не трудно убедиться непосредственной проверкой. Поэтому a = 0 и есть ответ на вопрос задачи.

На примере 5 хорошо видно, что решение сложной задачи — это не конная атака с шашками наголо, а скорее освобождение города от неприятеля, когда необходимо тщательно обследовать каждый дом, подвал, чердак.
Пусть принцип отсроченного действия будет твоим флажком, который поможет тебе избежать ошибок и ненужных действий. Помни, что это — ключ к успеху!

* Принцип — происходит от латинского слова «начало» или «основа». Этот термин употребляется в связи с самыми различными сферами человеческой деятельности и обозначает то, что лежит в основе рассматриваемых явлений. (Томилин А. Н. В поисках первоначального. — Ленинград: Детская литература, 1978. — С. 145.)

СОВЕТ 2. Принцип правильности решения, или «Чувство опасности»