Книгу с этим названием мы стали «придумывать» в 1999 году. В основу положили наш изобретательский и преподавательский опыт, а также известные учебные задачи из тризовских картотек. Тогда казалось, что год-два, — и работа будет сделана. Однако материал оказался очень «упрямым»! Запланированный график работ сломался…

Во-первых, стали сопротивляться задачи. По нашим соображениям, в сборник должны войти задачи:

• с интересным, желательно литературно хорошо изложенным сюжетом;
• имеющие изобретательскую или исследовательскую «изюминку»;
• посильные для решения школьниками;
• новые; или известные, но с новым решением.

Мы стали собирать факты из научной и популярной литературы и превращать их в задачи. Некоторые из них получались интересными, некоторые содержали исследовательскую «изюминку», некоторые удалось решить без высшей математики. Но вот чтобы все требования выполнялись сразу — с этим выходила загвоздка. Еще один момент сильно действовал на авторские нервы — после того, как найдена нужная подача условия и задача решена, всегда возникал вопрос — и это с этим-то мы мучались? Да ведь все «проще пареной репы». А потом приходила следующая задача — и опять споры и поиски. Пора сказать правду — каждый автор уверен, что именно его решение самое лучшее, и если мы пока еще не передрались, то это только потому, что каждый из нас чувствует укоризненный взгляд будущего читателя и его вопрос: ну когда же, наконец?

А во-вторых, оказалось, что нас опыт не достаточен. Мы и сами не всегда понимаем, как именно выходим на то или иное решение. А без этого трудно написать теоретическую часть книги, предложить методики.
Так что работа затянулась… Но мы, в очередной раз, не унываем и строим планы…

А пока рискнем представить на суд читателя несколько открытых задач. Не судите слишком строго…

ВЫПУСК 1

Задача 1. БЫСТРОЕ ПИТАНИЕ

В Черном море обитает один из видов рыб удильщиков¹
(см. рис. 1).

Рис. 1. Рыба-удильщик. Экспонат Зоологического музея
(Санкт-Петербург).

Обычно эта хищница лежит на дне и приманивает свои жертвы светящимся отростком, который болтается на кончике острого шипа, выступающего из ее головы. Прежде, чем поддавшаяся на приманку рыбка осознает свою ошибку, она уже оказывается в огромной пасти охотницы² . Как хищнице это удается, если сама она при этом остается на месте? Оцените время, в течение которого происходит заглатывание жертвы.

Решение

1. СИСТЕМНОСТЬ

В исследуемую систему входит: рыба-удильщик;
отросток-приманка; жертва, подплывшая к приманке, а значит к самим челюстям удильщика; другие рыбы; вода вокруг них; дно моря. В связи с тем, что рыба придонная, можно учитывать большой столб воды сверху.

2. ПРИЕМ ОБРАЩЕНИЯ

Как сделать, чтобы жертва оказалась в пасти хищницы? Затащить ее чем-то туда. Может быть языком, как лягушка ловит насекомых? А может быть, удильщик жертву гипнотизирует?

3. ИКР

Рыбка-жертва сама попадет в пасть удильщика, если:

• она сама захочет туда заплыть;
• ее занесет в пасть какая-то сила, возникающая, когда жертва подплывет к приманке.

4. ВЕЩЕСТВЕННЫЕ РЕСУРСЫ

• Может быть, в пасти удильщика есть еще одна, еще более «интересная» приманка. Тогда рыбка действительно сама поплывет в пасть.
• Какое вещество может затолкнуть жертву в пасть удильщика? Сам удильщик — но по условию он остается на месте. Это может сделать вода, если вместе с
  рыбкой-жертвой втянется в пасть.
• Можно еще представить себе, что жертву загоняют в пасть хищника другие рыбы, но это больше похоже на фантастический сюжет.

5. ПРОЦЕССЫ

Способствовать заглатыванию жертвы могут или процессы, сопровождающие приманивание (например, свечение, или шевеление языком, как будто это червячок), или процессы, способствующие попаданию воды вместе с рыбкой в пасть хищника. Таким процессом может быть перемещение жидкости.

6. ФОРМУЛИРОВКА ГИПОТЕЗ

a) Рыба-удильщик заманивает в пасть жертву какой-то второй приманкой, находящейся непосредственно в пасти.

б) Удильщик широко раскрывает челюсти, и жертва попадает в пасть вместе с водой благодаря разности давлений в пасти и в окружающей среде.

7а. ПРАВДОПОДОБНОСТЬ ГИПОТЕЗ

Обе гипотезы кажутся вполне правдоподобными. Действительно, существуют глубоководные рыбы, у который светящийся орган-приманка находится прямо в пасти.

Вторая гипотеза тоже правдоподобна. Во всяком случае, каждый, кто когда-нибудь открывал рот под водой, знает, как быстро попадает туда вода.

7б. ПРОВЕРКА ГИПОТЕЗ

Гипотезу а) можно проверить только экспериментально — поймав удильщика и изучив его внутреннее строение.

Гипотезу б) можно проверить оценочным расчетом.
Резко открывая пасть, удильщик создает внутри нее область низкого давления.

Дальнейшая картина понятна: жертва вместе с порцией воды стремительно втягивается внутрь охотницы. Попробуем оценить силу, с которой втягивается в пасть жертва с водой. Длину жертвы будем считать на порядок меньше длины самого удильщика — то есть 15 см. При такой длине поперечный размер рыбки-жертвы будем считать равным 5 см. То есть жертву вместе с непосредственно окружающей ее водой будем считать цилиндром длиной 15 см, диаметром 5 см и плотностью около 1000 кг/м³ (плотность воды). Глубину, на которой происходит все действие, будем считать равной примерно³
100 м (h = 100 м).

Силу, действующая на цилиндр (жертву) на такой глубине, можно рассчитать по формуле:

S — торцевая поверхность цилиндра.

Расчет по формуле (1) дает результат

Сила очень велика, и жертве с такой силой не справиться. Не зря одно из семейств удильщикообразных называют «морскими чертями».

Теперь попробуем определить время всасывания.

Ускорение, с который всасывается жертва, определим, используя 2-й закон Ньютона:

где F — уже подсчитанная нами сила, а m — масса жертвы, которую легко рассчитать:
.

Расчет по формуле (2) с учетом (3) дает ускорение примерно

Таким образом, жертва испытывает огромные перегрузки!

С другой стороны, движение жертвы в пасть можно описать формулой:

Подсчет по формуле (4) дает время заглатывания около

На первый взгляд трудно себе представить, что время заглатывания жертвы может быть таким кратким.

Комментарий
Если учесть, что открывание пасти занимает на самом деле некоторое время, то сила втягивания жертвы окажется меньше, а время заглатывания — больше. Однако вполне допустимо, что реально эта сила будет и побольше — ведь удильщик может обитать и на глубинах более 100 метров⁴. Скорость заглатывания также значительно зависит от величины жертвы.

Кстати, авторы в сети Интернет нашли такой факт: канадским биологам удалось измерить время заглатывания жертвы
рыбой-удильщиком.

А в одном из документальных видеофильмов серии BBC «Живая природа: эти загадочные животные» утверждается, что удильщик — самый «быстроглот» в природе, и время заглатывания пищи может иметь порядок 10^-4 с. Это не расходится с нашими расчетами — просто рекордный показатель мог быть измерен с более короткой жертвой или на большей глубине.

Точка роста

1. Выясните, как зависит скорость заглатывания жертвы от ее размеров?
2. Оцените, какое усилие развивает рыба-удильщик, раскрывая пасть? Кстати, поразмышляйте — уместно ли, решая этот вопрос, применить в качестве модели процесса простой рычаг?

Задача 2. СО ДНА МОРСКОГО

При океанологических исследованиях берут пробы грунта со дна океана. Для этого опускают на стальном тросе особый прибор. Необходимо с помощью такого устройства (прибор на стальном тросе) взять пробу грунта со дна Марианской впадины. Выдержит ли трос собственный вес? Как сделать, чтобы выдержал? Обоснуйте свое мнение расчетами.

Решение

Прежде всего, нужно разобраться, выдержит ли трос собственную тяжесть (весом прибора пренебрежем). Выясним, какие силы действуют на трос (см. рис. 2.1).

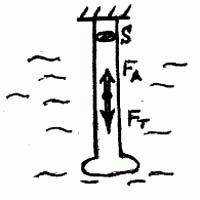
Рис. 2.1.

Это — сила тяжести:

и сила Архимеда:

Напряжение, которое выдерживает трос, равно:

Подставляя (1) и (2) в (3), получим:
.

Чтобы выяснить предельную глубину, нужно знать предел прочности стали. По таблице находим, что предельная нагрузка
Тогда из (3) находим h = 6000 м. Поскольку глубина Марианской впадины H = 11022 м, взятие пробы с ее дна с помощью стального троса кажется невозможным.

Если сделать что-то «невозможно», но очень хочется, то это изобретательская задача. Как сделать, чтобы трос не рвался? Взглянем еще раз на формулу (3) . Можно ли увеличить силу Архимеда?

Применив прием обращения: «Как сделать, чтобы увеличилась сила Архимеда, действующая на трос?», можно догадаться, что есть возможность «облегчить» трос, прикрепив к нему баллоны с воздухом (см. рис. 2.2).

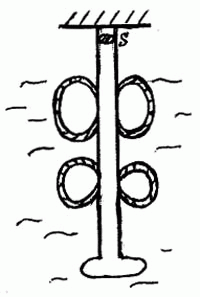
Рис. 2.2.

Прежде, чем рассчитывать эту конструкцию, подумаем, нельзя ли ее упростить. Можно ли «пустоту», которая находится в баллонах, ввести внутрь троса? Задав вопрос, как это сделать, можно увидеть более простую конструкцию: трос, полый внутри (см. рис. 2.3).

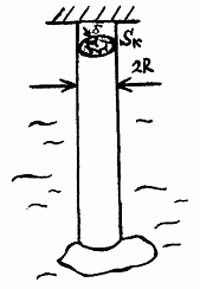
Рис. 2.3.

Выясним, какая должна быть толщина стенок троса

чтобы трос не оборвался под собственной тяжестью.

Запишем еще раз формулу (3):

Теперь в этой формуле

(площадь кольца в сечении троса при
).

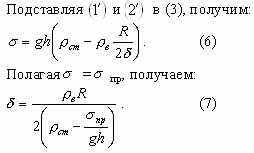
Подставив численные данные, имеем для Марианской впадины

Например, при радиусе троса 8,3 мм толщина стенок должна быть 1 мм.

Из формулы (7) видно, что в принципе можно достичь любой глубины, используя для троса материал любой прочности, если создать внутри него полость, удовлетворяющую условию (7).

Логично было бы сплетать подобные тросы из полых стальных ниток.

Возникает сомнение, выдержит ли полый трос давление воды на дне Марианской впадины. Оценим это давление:

Поскольку эта величина меньше предела прочности стали на сжатие, трос выдержит.

Точка роста

Оцените массу полого троса для Марианской впадины. Можно ли его изготовить?

Задача 3. ПЛАНЕТА МЫМРИКОВ

На некоторой планете живут мымрики. Планета имеет шарообразную форму и постоянно покрыта толстым слоем облаков. Космические пришельцы беспощадно эксплуатируют мымриков. Они развесили вокруг планеты отражатели и устроили круглосуточное освещение всей планеты. Пришельцы утверждают, что длина суток на планете составляет 36 часов, и заставляют мымриков работать 24 часа подряд и только
12 часов дают на отдых. Всем мымрикам пришельцы раздали электронные часы, и за опоздание на работу даже на
0,0001 с — крупный штраф.

Существует легенда, что в старые добрые времена сутки на планете составляли 24 часа, и тогда работали 12 часов и 12 — отдыхали. Как мымрикам определить длину суток, чтобы опротестовать продолжительность рабочего дня? Ведь на планете постоянно светло и облачно.

Примечания
1. Радиус планеты был определен мымриками в старые добрые времена на основе триангуляционных измерений.
2. Уровень развития мымрицкой техники и науки примерно совпадает с тем, который был на Земле в 30-е годы 20-го века.

Решение

Казалось бы, решение задачи невозможно. Как определить период вращения планеты, не имея возможности выглянуть за ее пределы? Ну что ж, попробуем опереться на свойства самой планеты.

Раз планета вращается, то вес тела на экваторе и полюсе различен, причем это отличие зависит от скорости вращения планеты. Эта скорость, в свою очередь, зависит от продолжительности суток. Это уже зацепка. Возникает идея: определить значения ускорений свободного падения на полюсе и на экваторе планеты и на основе их разницы рассчитать продолжительность суток. Тем более, что прибор для точного измерения g сделать очень легко — это математический маятник.

Итак, приступим. Прежде всего разберемся, как на основе разницы в значениях ускорения свободного падения на полюсе g_п и экваторе g_э определить длину суток.

Обозначим ускорение свободного падения на полюсе планеты g_п, а ускорение свободного падения на экваторе — g_э.

Величину g_э рассчитаем с учетом того, что каждое тело на экваторе принимает участие в движении по окружности. А значит, для этого тела II закон Ньютона примет вид (см. рис. 3):

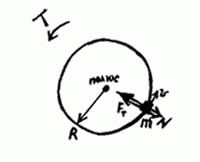
Рис. 3

Fт — N = ma_ц, (1)
где
Fт = mg_п (2)
( это сила тяжести без учета вращения, то есть на полюсе (напомним, что полюс не вращается).

Для точки, находящейся на экваторе планеты, центростремительное ускорение определяется по формуле:


точки благодаря вращению планеты,

Решая совместно три последних уравнения, имеем:

Из (4) видно, что

Таким образом, из последнего соотношения легко

Для маятника, расположенного вначале на полюсе, а затем на экваторе, мымрики могут экспериментально определить значения периодов T_п и T_э, а затем по формулам (6) и (7) рассчитать величины ускорения свободного падения на полюсе и на экваторе:

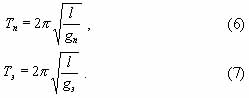
Подставив в (5) значения g, можно рассчитать период вращения планеты, или, другими словами, определить сутки.

Впрочем, мымрики могут догадаться и до более простого решения. Для определения величины суток им достаточно построить маятник Фуко⁵  — и тогда не надо будет делать сложных расчетов, да и погрешность в определении радиуса планеты тоже не помешает.

Точка роста

Если по формуле (5) рассчитать длительность суток на Земле, использовав значения g на полюсе и на экваторе из справочника, то получается 27 часов. Почему такое расхождение?

См. также:
Решебники открытых задач по физике и биологии
Теория открытых задач: проблематизация